3 Basics 2: Grundlæggende greb for den kvantitative historiker
Dette kapitel introducerer til, hvordan vi bruger nogle traditionelle kvantitative metoder i R. Det er ikke ment som en introduktion til kvantitativ metode eller statistik alment. Det er derimod en simpel guide til, hvordan du laver en håndfuld simple operationer, der kan gøre dig mere sikker i, hvad du siger med dine data.
Både dette og æste kapitel eksemplificerer ved hjælp af et enkelt datasæt - det samme vi brugte i forrige kapitel. Men nu har vi brug for lidt mere kontekst: Dette datasæt viser ophold i Stokhusslaveriet - et fængsel for lænkede, mandlige straffefanger i det nordlige København - fra 1741 til 1799. Det indeholder oplysninger om 3190 ophold og er skabt som del af et forskningsprojekt i fængslets tidlige historie i Danmark. Det er bygget på et mandtal holdt af skriveren ved fængslet. Datasættet blev ikke skabt med det formål at demonstrere programmeringsprincipper. Faktisk blev det slet ikke skabt med andre end mig selv in mente, og derfor har det idiosynkrasier. Som med næsten alt historisk materiale er det heller ikke fuldstændigt konsistent. På den måde ligner det et “ægte” datasæt skabt af en historiker (fordi det er det). Undervejs vil jeg give flere eksempler på huller, tvetydigheder eller andre problemer i dataene. Som historiker er disse knudrede punkter vigtige. De er som regel udtryk for, at vores data er levn af virkelige processer.
Vi starter derfor med at loade dette data ind. De kan hentes her:
# Vi loader pakker
library(tidyverse)
library(readxl)
# Vi loader også noget data
df <- read_excel("data/Slave_1741_1800_clean.xlsx")Hvordan ser vores data ud?
head(df)# A tibble: 6 × 16
Navn SLAVE…¹ Indko…² Udkom…³ Afslu…⁴ Fejls…⁵ Baggr…⁶ Ærlig…⁷ Relig…⁸ Alder
<chr> <dbl> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <dbl>
1 Morten … 1504 1741-0… 1741-1… Dead No fai… Army Uærlig Luther… 40
2 Hovel N… 1505 1741-0… 1741-0… Releas… No fai… Navy Ærlig Luther… 53
3 Peder L… 1506 1741-0… 1741-0… Releas… No fai… Navy Ærlig Luther… 26
4 Knud Ol… 1507 1741-0… 1741-0… Releas… No fai… Navy Ærlig Luther… 35
5 Lars La… 1508 1742-0… 1742-0… Releas… No fai… Civili… Ærlig Luther… 54
6 Mads Je… 1509 1742-0… 1742-0… Releas… No fai… Civili… Ærlig Luther… 63
# … with 6 more variables: Ægteskab <chr>, Kropsstraf_kat <chr>, Livstid <chr>,
# Tyv <chr>, Desertør <chr>, Brændemærket <chr>, and abbreviated variable
# names ¹SLAVE_ID, ²Indkommen, ³Udkommen, ⁴Afslutning,
# ⁵Fejlslagne_flugtforsøg, ⁶Baggrund, ⁷Ærlighed, ⁸Religion3.1 Gennemsnit, median, kvartiler
Når vi arbejder med taldata, har vi ofte brug for at vide noget om, hvordan vores data ser ud. Den fornemmelse kan vi få på mange måder. End af dem vi nok er allermest bekendte med, er gennemsnittet. I R finder vi et gennemsnit på en talværdi vha. af funktionen mean( ).
mean(df$Alder, na.rm = TRUE)[1] 33.97842Bemærk argumentet na.rm = TRUE. Dette er nødvendigt, fordi kolonnen Alder indeholder manglende værdier. Disse kan vores regnefunktion ikke håndtere. Argumentet fortæller således, at disse skal fjernes før vi laver udregningen.
Hvis man kan huske sin matematikundervisning fra folkeskolen, kan man måske huske, at gennemsnittet fås ved at lægge en serie af tal sammen og dividere med antallet af tal. Måske kan man også huske en formaning om, at gennemsnittet er vigtigt at kende, men kan forvrides af usædvanlige værdier, der hurtigt kan trække et gennemsnit langt i en retning. Jeg kan ikke huske mine matematiktimer. Det var mig vistnok principielt imod, at vi fik karakter i orden. Jeg har vanskelig. Men jeg har lært pointen senere hen. Tag nu for eksempel talserien 1, 1.1, 1.3, 1.8, 1.9, 4, 49. 5 af 7 værdier ligger under to, men hvad er gennemsnittet?
talrække <- c(1, 1.1, 1.3, 1.8, 1.9, 4, 49)
mean(talrække)[1] 8.585714I forhold til vores angivelser af alder, kunne man forestille sig, at der ikke skal mange 90-årige fanger til at skævvride billedet. Derfor har vi også et andet begreb, der kan bruges til at angive midtpunktet i data, nemlig medianen. Vi kan tænke medianen som det midterste tal, hvis vi lagde alle vores tal ud på en ordnet række fra lille til stor. Medianen er på den måde det tal, der bogstaveligt talt er det midterste i en række af tal, hvorimod gennemsnittet på sæt og vis er en model, der stipulerer et teoretisk centrum, der ikke nødvendigvis eksisterer. Hvad er medianen i vores talrække?
median(talrække)[1] 1.8Her er der altså stor forskel på median og gennemsnit. Hvordan ser det ud med alderen på fangerne?
median(df$Alder, na.rm = TRUE)[1] 31Medianen er altså næsten tre år mindre end gennemsnittet. Dette antyder, at der er mange relativt unge fanger, men at et mindretal af ældre fanger påvirker tallene.
Hvor medianen angiver det midterste tal i en række af sorterede observationer findes tilsvarende begreber for de tal man finder 25% og 75% af vejen igennem rækken. Disse kaldet kvartiler (nedre og øvre kvartil). Disse finder vi med en tilsvarende funktion.
quantile(df$Alder, na.rm = TRUE) 0% 25% 50% 75% 100%
15 25 31 40 92 Tallet for 50% angiver medianen. Tallet for hhv. 0% og 100% den mindste og største værdi i rækken. Man kunne altså komme i slaveriet allerede som 15-årig - men også som 92-årig (hvis kildens angivelse er til at stole på).
Ofte vil vi have behov for at udregne gennemsnit og/eller median på forskellige kategorier (der angives i en anden kolonne). Det kan gøres ved at gruppere og så udregne ved hjælp af funktionen summarise.
df %>%
group_by(Baggrund) %>%
summarise(Gennemsnit = mean(Alder, na.rm = TRUE),
Median = median(Alder, na.rm = TRUE),
Standardafvigelse = sd(Alder, na.rm = TRUE))# A tibble: 6 × 4
Baggrund Gennemsnit Median Standardafvigelse
<chr> <dbl> <dbl> <dbl>
1 Army 31.0 29 9.17
2 Civilian 36.4 34 13.3
3 Navy 30.9 27 11.3
4 Recidivist 36.1 34 10.9
5 Transfer 39.5 37 13.9
6 <NA> 42.2 40 16.1 Her ser vi f.eks., at eks-militære fanger ofte var yngre end resten af fangebefolkningen. Vi har også introduceret endnu et mål - standardafvigelsen - der findes med funktionen sd( ). Den fortæller os, hvor meget data spreder sig. Simpelt forstået som en indikator på, om data klumper sig sammen tæt om den gennemsnitlige værdi (lavere scorer for standardafvigelse) eller er smurt grundigt ud (højere scorer). Her ser vi, at standardafvigelsen er lavest for eks-soldater (hvilket måske antyder, at der ikke var så mange gamle soldater i 1700-tallets stående lejehær (og at dem, der var ofte havde accepteret deres skæbne som del af garnisonsbyernes laveste sociale lag, og derfor ikke pludseligt tyede til hård kriminalitet).
3.2 Antalstabeller og chi2-test
Som historikere arbejder vi ofte med data, der indeholder forskellige kvalitative variable. Her er vores observationer typisk inddelt i forskellige kategorier. Ved at tælle, hvordan observationer fordeler sig på tværs af kategorier, prøver vi at sige noget om, hvorvidt der er mønstre i vores data. Med mønstre mener vi ofte, at der er en sammenhæng imellem forskellige variable. F.eks.: er der mon en sammenhæng imellem fangernes baggrund før fængslingen (der kan være inddelt i en række forskellige kategorier), og det at have modtaget en kropsstraf i forbindelse med indsættelsen? Disse typer af oplysninger ville typisk eksistere i to forskellige kolonner med hvert sit sæt af kategorier - hvilket også er tilfældet her. Vi kan så krydse imellem dem og for hver kategori i én kolonne, tælle hvor mange observationer, der lander i hver af den anden kolonnes kategorier.
Ofte er det imidlertid ikke nok bare at tælle, hvordan observationerne fordeler sig på tværs af disse kolonner. Vi kan være usikre på, hvorvidt det giver mening at tale om en sammenhæng eller ej, og om hvilken betydning vi kan tillægge, det mønster vi identificerer. I sådan en kontekst kan vi bruge en statistisk test, nemlig den såkaldte chi2-test (udtalt “chi-i-anden”, på engelsk “chi-squared test”). Denne test sluger som udgangspunkt en antalstabel, der fortæller hvordan observationer fordeler sig på forskellige kategorier. Ud spytter den så en indikator for, hvorvidt der er sammenhæng imellem vores variable. Vi kan tænke det sådan, at testen afprøver om det mønster vi ser i vores antalstabel er statistisk signifikant. Dette er særligt vigtigt, hvis vores data er et sample, for så har vi brug for en indikator, der fortæller os, hvor meget vi bør stole på, at de mønstre vi finder i vores sample også ville være at finde i den fulde population, vores sample bygger på. Men det kan også være interessant at bruge testen, selvom vi faktisk har et komplet datasæt over en population. Her giver testen os en fornemmelse for hvor sandsynligt det er, at et observeret mønster er en tilfældighed, der ligeså godt kunne have set anderledes ud.
Så hvordan laver man en chi2-test? Hver række repræsenterer en fanges ophold i fængslet. Datasættet består primært af kategoriserede data. For at udforske sammenhænge imellem disse mange variable har vi brug for at lave antalstabeller. Nedenfor bruger vi tidyverse-funktioner til at tælle observationer ifht. to variable, henholdsvis variablen “Baggrund” (der fortæller om en fanges baggrund før indsættelsen) og variablen “Kropsstraf_kat” (der fortæller om fangen før indsættelsen havde modtaget korporlig straf).
baggrund_kropsstraf <- df %>%
group_by(Baggrund, Kropsstraf_kat) %>%
summarise(n = n()) %>%
spread(Kropsstraf_kat, n) %>%
na.omit() %>%
column_to_rownames(var = "Baggrund")
print(baggrund_kropsstraf) Corporal punishment No corporal punishment
Army 743 438
Civilian 364 821
Navy 292 145
Recidivist 26 58
Transfer 118 144Det kan være nyttigt at kunne denne funktionalitet vha. tidyverse-funktioner, da vi dermed forstår de skridt, det implicerer (gruppering, optælling, spredning af observation på kolonner, fjernelse af NA-værdier). Der er imidlertid en lettere måde at lave antalstabellen på. Denne giver os tilmed tabellen i et helt rent format, så den passer til det test-funktionen forventer.
min_antalsttabel <- as.data.frame.matrix(table(df$Baggrund,
df$Kropsstraf_kat))
print(min_antalsttabel) Corporal punishment No corporal punishment
Army 743 438
Civilian 364 821
Navy 292 145
Recidivist 26 58
Transfer 118 144Forskellen på de to tabeller er simpel. Første kolonne er konverteret til egentlige rækkenavne og rækken, der talte antallet af NA-værdier er filtreret fra. Nu er vi klar til at udføre selve testen.
chisq.test(min_antalsttabel)
Pearson's Chi-squared test
data: min_antalsttabel
X-squared = 318.1, df = 4, p-value < 2.2e-16Testen spytter tre tal ud. Det vi i udgangspunktet skal forholde os til er p-værdien. Denne fortæller os groft sagt, hvor sandsynligt det er, at de observerede variable er uafhængige. P-værdien er 1, hvis der er 100% statistisk sandsynlighed for, at vores variable er uafhængige af hinanden. Desto lavere p-værdien er (tættere på 0), desto mere sandsynligt er det, at der er en sammenhæng mellem de to variable. Der er tradition for, at en p-værdi på mindre end 0.05 regnes for statistisk sandsynlig. Det betyder ikke, at et mønster med en højere værdi ikke kan bære nogen betydning, blot at vi ikke kan bruge statistikken som belæg herfor. I dette tilfælde er p-værdien angivet som “mindre end” 2.2e-16. Det vil altså sige mindre end 0.00000000000000022. Når p-værdien under 2.2e-16 spytter testen ikke den specifikke værdi ud, men siger blot, at den er mindre end dette meget, meget lille tal. Da 0.00000000000000022 er mindre end 0.05 kan vi derfor sige, at vores data kan give statistisk belæg for at sige, at der er en sammenhæng imellem en fanges baggrund og eventuelle kropsstraffe. Læg mærke til, at vi dermed ikke kan sige noget om, hvad denne sammenhæng består i. Vi ved blot, at der er en sammenhæng af en slags, og den kan vi så undersøge videre.
Fordi datasættet har flere tusinde observationer, vil mange af de antalstabller vi kan lave med datasættets forskellige variable give en lav p-værdi - og dermed vil vi kunne pege på mange sandsynliggjorte sammenhænge. Når vi har mange observationer, kan selv subtile mønstre siges at være betydningsfulde, fordi vi dermed har en større sikkerhed for, at det ikke blot er en tilfældig fordeling. Testen er måske særligt nyttig, når vi arbejder med små datasæt, hvor vi er i tvivl om, hvorvidt et mønster er signifikant eller ej. Der er dog også sammenhænge i vores data, der giver et andet resultat, trods størrelsen. F.eks.:
as.data.frame.matrix(table(df$Ægteskab,
df$Tyv)) %>%
chisq.test()
Pearson's Chi-squared test with Yates' continuity correction
data: .
X-squared = 2.234, df = 1, p-value = 0.135Her tester vi, om der er en sammenhænge mellem, hvorvidt en fange er dømt for tyveri, og om han er gift. Selvom vi måske ville synes, at vi så et mønster ved at kigge på de rå tal, indikerer testen her, at vi ikke kan afvise, at dette mønster er tilfældigt.
3.3 Korrelationstest
En andet hyppigt brugt greb blandt kvantitative historikere er test af korrelation. Denne test tager to numeriske variable og tester graden af korrelation (hvilket vi måske kan oversætte som sammentræf). Firkantet sagt kan vi tænke det sådan, at den leder efter et mønster. Når variabel A er større end sit gennemsnit, er variabel B så også højere? Hvis dette typisk er tilfældet taler vi om en positiv korrelation. Hvis variabel A typisk er mindre end sit gennemsnit, når den for variabel B er højere (eller omvendt), vil vi modsat tale om en negativ korrelation.
Den såkaldte korrelationstest, der ligesom chi-i-anden-testen er designet af Karl Pearson i starten af det 20. århundrede, giver os en score, der fortæller hvor stærk eller svag korrelationen er, og om den er positiv eller negativ. Test-scoren svinger fra +1 til -1.
+1 betyder at der er en perfekt positiv korrelation.
0 betyder, at der ikke er nogen korrelation.
-1 betyder at der er en perfekt negativ korrelation.
I det datasæt, der bearbejdes i dette kapitel findes den numeriske variabel “Alder”. Den fortæller den alder, der er angivet for hver fange ved indsættelsen. Det er et tal, vi ikke skal stole blindt på, da mange fanger ikke har kendt deres præcise alder og derfor er der en tendens til runde tal. Alligevel giver angivelserne nok et nogenlunde rimeligt billede af fangernes alder. Vi kunne måske i den forbindelse tænke os at vide, hvorvidt et fængselsopholds varighed korrellerer med alder. Hvis det f.eks. var sådan, at de ældre fanger typisk sidder med lange domme og ikke løslades, kunne vi forvente en positiv korrelation. Hvis det modsat var sådan, at ældre fanger døde før straffen var fuldført - hvilket heller ikke er en urimelig hypotese grundet forholdene i fængslet - kunne dette måske udtrykke sig i en negativ korrelation, fordi yngre fangers ophold så ville blive længere.
For at kunne lave denne udregning har vi brug for en variabel, der angiver hvert opholds varighed. Dette kan vi heldigvis nemt udregne, fordi lubridate-pakken gør det muligt at arbejde og regne med datoer. Funktionerne er introduceret i forrige kapitel.
library(lubridate)
Alder_varighed <- df %>%
mutate(Ankomstdato = ymd(Indkommen),
Slutdato = ymd(Udkommen),
Varighed = Slutdato - Ankomstdato,
Varighed = as.numeric(Varighed)) %>%
select(Alder, Varighed) %>%
na.omit()Warning: There was 1 warning in `mutate()`.
ℹ In argument: `Slutdato = ymd(Udkommen)`.
Caused by warning:
! 5 failed to parse.Vi kan se, at den nye tabel ikke har ligeså mange observationer. Vi har mistet lige under 200 observationer. Dette skyldes, at der i enten kolonnen “Indkommen” eller “Udkomme” har været en NA-værdi. Dette (relativt beskedne) antal af manglende værdier må vi acceptere. Manglende værdier er næsten altid et vilkår, når vi arbejder med historiske data.
Vi har nu en tabel med to kolonner med talværdier: Alder og Varighed. Nu er vi med andre ord klar til at køre selve testen.
cor.test(Alder_varighed$Alder, Alder_varighed$Varighed)
Pearson's product-moment correlation
data: Alder_varighed$Alder and Alder_varighed$Varighed
t = -3.2488, df = 3098, p-value = 0.001171
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.09328325 -0.02311305
sample estimates:
cor
-0.05827012 Testen giver os en lang række scorer, vi må forholde os til. Den vigtigste er korrelationskoefficienten, der her findes til sidst under “cor”. Den er -0.058. Her er altså en meget svag negativ korrelation. Traditionelt taler man om en svag positiv korrelation, hvis værdien er over 0.1, en moderat positiv korrelation når scoren er over 0.3 og en stærk korrelation, når scoren er over 0.5. Tilsvarende negative værdier giver så den tilsvarende angivelse af styrken af en negativ korrelation. Her er vores score altså under det man normalt ville kalde bare en svag korrelation.
At vi er tæt på 0 fortæller os altså, at der ikke er nogen umiddelbar sammenhæng imellem alder og varighed af fængselsopholdet. Vi får mao. ikke noget umiddelbart statistisk belæg for vores hypoteser fra tidligere, hverken den ene eller den anden.
Hvor sikker er vi så på denne score? Igen får vi her også en p-værdi. Den er lav: 0.001171. Også her angiver p-værdien sandsynligheden for, at vores test-resultat er et udtryk for en statistisk tilfældighed. Dermed kan vi sige, at dette er højst usandsynligt. Vi har så mange observationer, at vores testscore har en høj statistisk pålidelighed, og vi er derfor temmelig sikre på, at fraværet af korrelation må tages alvorligt. En fanges alder og fængselsopholdets varighed korrelerer ikke. Testen giver os ydermere et såkaldt 95% konfidensinterval. Dette er en anden måde at udregne pålideligheden af data. Dette interval (der angives af en minimums- og en maksimumsværdi) fortæller os, at med 100 samples af tilvarende data, ville vi statistisk forvente at få en score indenfor dette interval i minimum 95% af tilfældene.
Korrelationstesten er et velkendt værktøj. Og det er relativt nemt at forstå, hvad det fortæller. Alligevel ser man fra tid til anden, at folk argumenterer for, at en stærk korrelation (omend den er positiv eller negativ) fortæller noget om kausalitet - at en variabel forklarer en anden. Dette kan godt være korrekt, men er grundlæggende ikke testens sigte, og det er derfor ikke det, den fortæller os. Korrelation kan ligeså vel skyldes at både variabel A og variabel B forklares af en tredje variabel. Testen fortæller os således blot, hvorvidt der er et mønster eller ej. Det er op til os at fortolke det.
3.4 Lineær regression
Korrelationskoefficienten fortæller os intet om hvad, der forklarer hvad (eller om noget overhovedet kan forklares). Har vi rimelig antagelse om, at en (eller flere) variable kan forklare en anden, kan vi foretage en regressionsanalyse. Der findes et væld af forskellige former heraf. I denne kontekst vil jeg blot demonstrere den nok mest simple: lineær regression, hvor vi undersøger forholdet imellem to numeriske variable.1 Lad os fortsætte med at undersøge relationen imellem fængselshopholdets varighed og fangens alder ved ankomsten. Men lad os prøve at eliminere den påvirkning, der må forventes at komme ved, at fanger kom fra forskellige dele af samfundet, med hver deres jurisdiktion. Vi isolerer derfor de fanger, der havde en civil baggrund.
Det virker ikke helt urimeligt at antage, at Varighed kan forklares af Alder. Hvis ældre fanger blev slidt op af straffearbejdet eller døde af de tilbagevendende epidemier, der fik frit lejde blandt fangerne grundet fængslets kummerlige forhold, kunne dette måske udtrykke sig på netop denne måde. Når vi laver en model udtrykkes denne ofte som en formular: det vi formoder kan forklares ~ det vi formoder kan forklare. I denne kontekst bliver vores formular derfor Varighed ~ Alder.
df <- df %>%
mutate(Ankomstdato = ymd(Indkommen),
Slutdato = ymd(Udkommen),
Varighed = Slutdato - Ankomstdato,
Varighed = as.numeric(Varighed))
Alder_varighed_civile <- df %>%
filter(Baggrund == "Civilian") %>%
select(Alder, Varighed) %>%
na.omit()
lm(Varighed~Alder, Alder_varighed_civile)
Call:
lm(formula = Varighed ~ Alder, data = Alder_varighed_civile)
Coefficients:
(Intercept) Alder
1347.28 -12.77 Her får vi 2 mål for vores lineære model: Intercept fortæller os, hvor på y-aksen den lineære model skærer ved værdien 0 på x-aksen. Den anden score fortæller hvor meget linjen falder eller stiger for hver gang værdien på x-aksen vokser med 1. Modellen fortæller os med andre ord, at for hver gang en nyankommen fanges alder stiger med 1 falder varigheden af opholdet med et bestemt antal dage.
Vi kan til hjælp forsøge at visualisere. Teknikken til visualisering bliver gennemgået i næste kapitel.
ggplot(Alder_varighed_civile) +
geom_smooth(aes(x = Alder, y = Varighed), method = "lm", se = FALSE)`geom_smooth()` using formula = 'y ~ x'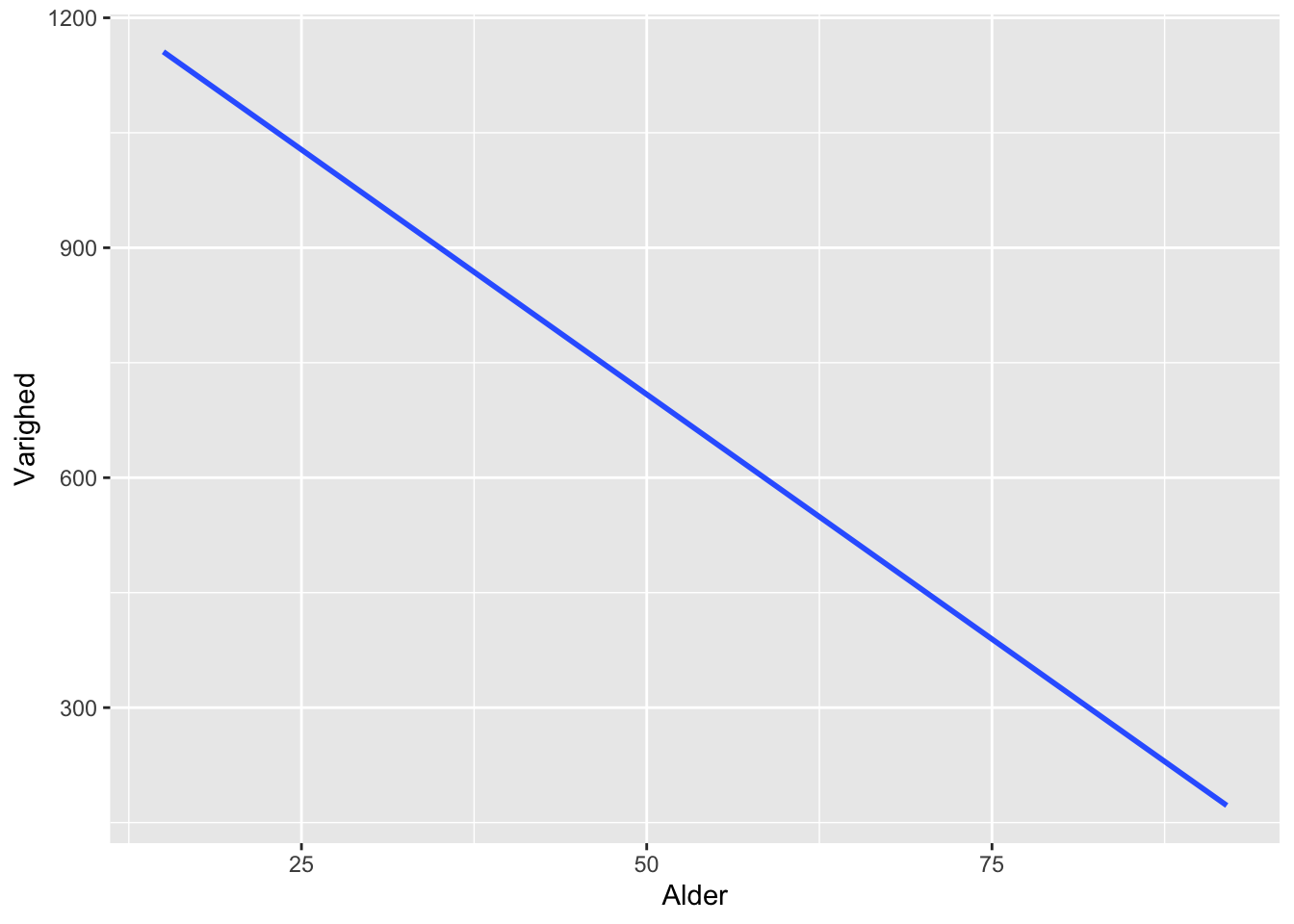
Modellen giver umiddelbar mening. Linjen kan på den måde hjælpe os til at forstå hvordan vores data ser ud. Imidlertid maskerer den åbenlyst, at vores data indeholder en masse varians: Fængselsopholdenes varighed svingede fra enkelte dage til årtier. Modellen viser den linje, der passer bedst til dette mønster, men det betyder ikke, at udsvingene ikke skal tænkes med. Et vigtigt spørgsmål bliver derfor, hvilken statistisk værdi vi kan tillægge modellen? Eller sagt på en anden måde, hvor godt kan Alder faktisk forudsige Varighed? Det kan vi undersøge ved at se på nogle flere scorer:
summary(lm(Varighed~Alder, Alder_varighed_civile))
Call:
lm(formula = Varighed ~ Alder, data = Alder_varighed_civile)
Residuals:
Min 1Q Median 3Q Max
-1110.4 -754.2 -494.9 109.6 10550.4
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1347.277 120.153 11.213 < 2e-16 ***
Alder -12.771 3.105 -4.114 4.17e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1400 on 1157 degrees of freedom
Multiple R-squared: 0.01442, Adjusted R-squared: 0.01356
F-statistic: 16.92 on 1 and 1157 DF, p-value: 4.168e-05Her er mange værdier, og det er for omfattende at gennemgå dem alle. Lad os fokusere på nogle få nøgleværdier:
P-værdien kender vi allerede. Den kan i denne kontekst tolkes på nogenlunde samme måde som i vores chi2-test: Den fortæller os, at der er en meget lille sandsynlighed for, at det observerede mønster er en tilfældighed. Denne sikkerhed skyldes, at vi har forholdsvis mange observationer. Vores resultat er altså statistisk signifikant.
Imidlertid har vi også en anden score vi må forholde os til: Den såkaldte R-squared (R2). Denne værdi fortæller os, hvor meget af variansen i variablen Varighed, der er bestemt af variablen Alder. Typisk ligger denne værdi imellem 0 og 1, der så kan tolkes sådan, at den forklarende variabel bestemmer mellem 0% og 100% af variansen. I dette tilfælde er vores R2-værdi ganske beskeden. Selvom vores model har statistisk signifikans (og dermed ikke må regnes for en tilfældighed) forklarer den altså kun en lille flig af dataene. Eller sagt på en anden måde, vi kan i statistisk forstand være ganske sikre på, at værdien for Alder kan kun sjældent forudsige værdien for Varighed.
Hvor høj en R2-værdi skal være, før vi antager, at vores model faktisk kan bruges til at forklare eller forudsige noget, varierer afhægigt af kontekst. Af samme grund er en aflæsning af R2 ofte et spørgsmål om at sammenligne med henblik på at finde de faktorer, der har den største forklaringsevne eller at sammenligne den samme faktors forklaringskraft i forskellige kontekster eller perioder. Alligevel kan vi også bruge modellen her. For den fortæller os noget: den antyder, at vi må søge andre, eventuelt kvalitative, forklaringsmuligheder.
3.5 Måske noget om logistisk regression
Df_uden_NA <- df %>%
mutate(Død = ifelse(Afslutning == "Dead", 1, 0)) %>%
select(Død, Ægteskab, Ærlighed) %>%
na.omit()
logistisk_model <- glm(Død ~ .,
family = binomial(),
data = Df_uden_NA)
summary(logistisk_model)
Call:
glm(formula = Død ~ ., family = binomial(), data = Df_uden_NA)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.0064 -0.5491 -0.5491 -0.5474 1.9860
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.822267 0.107944 -16.882 <2e-16 ***
ÆgteskabUnmarried 0.006418 0.115530 0.056 0.956
ÆrlighedUærlig 1.399224 0.101317 13.810 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 3044.7 on 3143 degrees of freedom
Residual deviance: 2862.9 on 3141 degrees of freedom
AIC: 2868.9
Number of Fisher Scoring iterations: 4confint(logistisk_model)Waiting for profiling to be done... 2.5 % 97.5 %
(Intercept) -2.0381640 -1.614748
ÆgteskabUnmarried -0.2174149 0.235770
ÆrlighedUærlig 1.2004246 1.597722exp(coef(logistisk_model)) (Intercept) ÆgteskabUnmarried ÆrlighedUærlig
0.1616588 1.0064382 4.0520542 De grundlæggende antagelser bag regressionsanalysen er diskuteret af Claire Lemercier og Claire Zalc i Quantitative Methods in the Humanities: An introduction (Charlottesville: University of Virginia Press, 2019), 73-87. En grundig praktisk gennemgang findes i Charles H. Feinstein og Mark Thomas, Making History Count: A primer in quantitative methods for historians (Cambridge: Cambridge University Press, 2002)↩︎